タイミングベルトにおける初期取付張力と駆動時の張側／緩み側張力の関係を教えてください

タイミングベルトにおける、初期取付張力と駆動時の張側／緩み側張力の関係式およびなぜそうなるか考え方について教えてください．
タイミングベルトの初期取り付け張力と，駆動時の張側／緩み側張力の関係について，以下の同径プーリを用いた系にて解説いたします．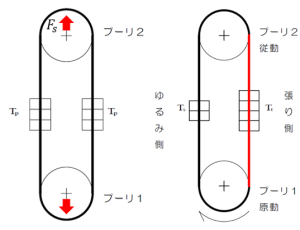
まず，ベルトを初期張力T_Pにてプーリに取り付けた場合を考えます（上図左側）．この際，当然ですが張側張力T_t，緩み側張力T_sの差異は無く，T_t = T_s = T_Pの関係が成り立ちます．一方，プーリ１とプーリ２の軸に作用する力F_s（軸間力）を考えれば，力のつり合いから
   F_s = 2 T_P = T_t + T_s
の関係が成立します．
次に，原動プーリ（プーリ１）に負荷（トルク）T_qを与えると，２つのプーリをつなぐベルト間に張力差が生じ，張り側では張側張力T_tが，緩み側では緩み側張力T_sがベルトに作用します．（上図右側）
ここで，ベルトの有効張力T_e = T_t - T_sは，T_qの大きさによって変化し，
T_q = T_e \times r
の関係が成立します．ここで，rはプーリの半径となります．
また，T_eとF_sを用いますと，T_tとT_sはそれぞれ
   T_t = \frac{F_s + T_e}{2}
   T_s = \frac{F_s - T_e}{2}
と表すことができます．
以上の関係から，T_qを増加させた場合，プーリの半径が一定であればT_eは増加します．ここでF_sが一定とすれば，T_qの増加に伴って，T_tは増加し，T_sは低下します．
計算上T_sが0を下回る（実際にはT_sは0付近を維持します）と，この質問にありますように，歯飛びなどの不具合が発生しやすくなります．また，上記リンクを御覧頂ければ，T_qの変化に伴うT_t，T_sの変化などがご確認頂けます．
当該内容については「新版　ﾍﾞﾙﾄ伝動・精密搬送の実用設計」養賢堂出版にも詳しく記載されておりますので、ご確認いただければと思います．

 

3 票, 平均: 1.00 / 1 3 人が参考になったと評価しました
この回答は参考になりましたか？良ければクリックください参考になった
読み込み中...